Q & A
- 基礎編
- 測定編
- Q1. どのような電極を使ったらいいですか?
- Q2. 基準電極はどこにつけたらいいですか?
- Q3. 両耳朶連結基準はよくないのですか?
- Q4. 電極配置について,以前の10-20法と新しい10%法はどこが違いますか?
- Q5. 電極帽を使うときに気をつけることは?
- Q6. ERPを記録するときのフィルタ設定はどうしたらいいですか?
- Q7. 短い時定数で記録したデータで長潜時成分を検討できますか?
- Q8. サンプリング周波数はどのくらいにしたらいいですか?
- Q9. ERPの測定には,どのくらい試行数がいりますか?
- Q10. どのくらいの時間を記録したらよいでしょうか?
- Q11. ベースラインはどのくらいの長さがいいでしょうか?
- Q12. ERPを安価で測定するためのシステムはありますか?
- Q13. 安価な刺激装置はありませんか?
- 統計分析編
- 論文投稿編
基礎編
Q1. ERPは何を反映しているのですか?
Q2. 得られたデータはどのように解釈するのですか?
Q3. ERPの「成分」とは何のことですか?
Q4. ERPはどのような研究に用いられていますか?
Q5. ERPはその他の脳機能測定法とはどのように違うのですか?
これらについては,ERPについての解説記事(PDF)を参照してください。工学心理学とERPについての総説記事(PDF)にも,ERPの基礎知識を載せています。これらの記事を改訂したものが「心理学のための事象関連電位ガイドブック」です。
Q6. ERP研究のための必読文献はありますか?
心理生理学会(Society for Psychophysiological Research: SPR) から「人間の事象関連電位を認知研究に利用するためのガイドライン:記録の標準規格と発表の基準 (Guidelines for using human event-related potentials to study cognition: Recording standards and publication criteria)」が2000年に発表されました。その題名から分かるように,このガイドラインには記録や分析の技術的側面だけでなく,ERPの研究報告が科学論文として認められるために必要な条件が詳しく述べられています。Psychophysiology誌からダウンロードできます [DOI]。SPRの許可を得て全訳したものを「心理学のための事象関連電位ガイドブック」の付録に収載しています。
これに先だって,1993年には,「研究文脈における脳電位活動の記録と量的分析のためのガイドライン (Guidelines for the recording and quantitative analysis of electroencephalographic activity in research contexts)」が発表されています。自発的に生じる背景脳波を測定・分析するときの注意点が述べられています。この論文も,Psychophysiology誌からダウンロードできます [DOI]。
さらに,2013年10月には,「委員会報告:脳波・脳磁図研究のための出版ガイドラインと勧告(Committee report: Publication guidelines and recommendations for studies using electroencephalography and magnetoencephalography)」がPsychophysiology誌に発表されています[DOI]。21ページにわたる詳細な資料です。
最近出版された洋書として,
- Handy, T. C. (Ed.). (2005). Event-related potentials: A methods handbook. Cambrige: MIT Press.
- Luck, S. J. (2005). Introduction to the event-related potential technique. Cambrige: MIT Press.
改訂版が出ました(2014年4月27日追加)。
Luck, S. J. (2014). Introduction to the event-related potential technique (2nd ed.). Cambrige: MIT Press.
があります。特に後者は,視覚ERPの研究で有名な研究者が単著で書いた優れた入門書です。この本が出ることを知っていたら,私は自分で本を書かずに,この本を翻訳したでしょう。
ERPを含む脳の電気活動についての最近の本に,
- Nunez, P. L., & Srinivasan, R. (2006). Electric fields of the brain: The neurophysics of EEG (2nd. ed.). New York : Oxford University Press. [電子ブック Google Books]
があります。Nunezによる名著(1981年)の改訂版です。必読ではないですが,詳しく知りたいときに参照するといいでしょう。
何年も前から出版のうわさがあった本が,ようやく出版されていました。
- Luck, S. J., & Kappenman, E. S. (Eds.) (2012). The Oxford handbook of event-related potential components. New York : Oxford University Press.
ペーパーバックでも15,000円以上しますが,ERP研究者なら手元に置いておきたい本です。
測定編
Q1. どのような電極を使ったらいいですか?
銀-塩化銀(Ag/AgCl)電極の電気特性がよいと一般に言われています。このほかにも,スズ(Sn,tin)電極,銀(Ag)電極などが使われていますが,これらは短い時定数(0.3秒)で記録する通常の脳波向けです。ERPのような緩やかな電位変化を長い時定数で記録するときには,Ag/AgCl電極を使うのが定番になっています。現在のAg/AgCl電極は焼結(sintered)タイプが主流で,壊れにくく,手入れも簡単です。
ただし,Ag/AgCl以外の電極でも,脳波計の入力インピーダンスが十分に高ければ(100MΩ程度:通常市販されている脳波計ならばこの程度はある),長い時定数でもあまり歪みなく記録できます(Picton, T. W., Lins, O. G., & Scherg, M. 1995. Handbook of neuropsychology (Vol. 10, p. 5), Elsevier: Amsterdam)。
Q2. 基準電極はどこにつけたらいいですか?
基準電極は,耳朶(じだ:earlobe)や鼻尖(nosetip)につけることが多いです。理論的には,基準電極は脳電位の影響を受けない場所につけるのですが,首から上にそのような場所はありません。頭部以外(首の付け根)に基準電極をおく方法もありますが,そうすると心臓に近くなるので心電位が混入します。また,頬やあごなど筋肉があるところでは筋電位が混入します。脳電位・心電位・筋電位の影響を比較的受けにくい場所を消去法で探していくと,耳朶や鼻尖が基準部位の候補として残るのです。
図1は,両耳朶連結と鼻尖を基準にして記録したERP波形の比較です。鼻尖を基準としたときには前頭極(Fpz)での振幅が小さくなっています。一般に,基準電極に近い部位の電位は小さく記録されます。本来ニュートラルであるべき基準電極に,測定している信号が漏れ込むからです。これを「基準電極の活性化」といいます。脳波は,基準電極と探査電極の間の電位差を測定したものですから,基準電極と探査電極に共通に含まれる電位は記録されません。そのため,基準電極に近い部位の電位は小さく見積もられるのです。
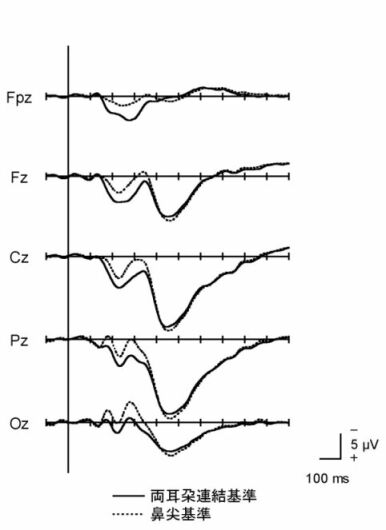
図1.ERP波形に及ぼす基準電極の影響。視覚3刺激オドボール計数課題におけるターゲット(p = .125)に対する16名の総加算平均波形。正中線上5部位における刺激呈示開始後1秒間の波形を示している。アナログ脳波計を用いて記録時から基準電極を変えて記録した(時定数3.2秒,ハイカットフィルタ30Hz,サンプリング周波数 200 Hz)。
マストイド(mastoid:乳様突起[耳の裏の付け根の頭蓋骨の突起])を基準部位とすることがありますが,マストイドは頭皮上にあり,耳朶よりも脳に近いので,側頭部の脳電位が漏れ込んできます。そのため,基準部位としてはあまりお薦めできません。側頭部で大きく記録される電位(P3も含みます)をマストイドを基準として記録すると,鼻尖を基準として記録したときよりも振幅が小さくなります。マストイドで基準電極の活性化が起こるからです。むしろ,マストイドには探査電極をおいて側頭部の電位を記録するのがよいでしょう。
このような基準部位の影響をなくすために,記録に使ったすべての電極で得られた電位の平均値を基準とする方法(平均基準)もあります。この方法は,頭部全体を覆うように均等な間隔でとりつけた複数の電極から脳波を記録するときには有効です。頭皮上電位分布図(トポグラム)を描いたり,電位発生源を推定するときに使われます。しかし,少ない部位から記録するときには平均基準は意味がありません。
波形をデジタル(数値)化しておけば,分析時に基準部位を変えることができます。記録時には,任意の部位を共通の基準として,残りの部位からデータを記録します。記録時に使う仮の基準電極はどこに置いてもよく,脳波電極とは別の電極をつけることも,脳波電極と兼用する(FzやCzなど)ことも,後で基準として利用する電極を使う(A1またはA2)こともあります。分析時に基準としたい部位(A1,A2,鼻尖など)にも電極をつけて,共通の基準との間の電位差を記録しておきます。大事なことは,すべての電極部位から共通の基準を使って記録することです。まばたきや眼球運動をモニタするのに,眼窩の上下/左右から眼電図を双極導出することがありますが,記録チャネルが余っているなら,上下左右の電極から別々に記録しておくことを薦めます。分析時に双極導出波形に計算しなおすことができます。左電極のチャネルには[左電極-システム基準]の電位差,右電極のチャネルには[右電極-システム基準]の電位差が記録されていますから,左右双極導出の波形[左電極-右電極]は,両者を引算することで求められます([左電極-システム基準]-[右電極-システム基準]=[左電極-右電極])。特に,眼窩上部の電極からは眼電位だけでなく脳電位も記録されるので,双極導出で記録した垂直眼電図には,眼電位だけでなく脳電位も含まれることになります。双極導出で記録した波形をあとから電極ごとに分解することはできないので,眼球アーチファクトを過大評価しないためにも,それぞれの電極を独立に記録するのが望ましいのです。
最初に述べたように,絶対に正しい基準部位というのはありません。基準電極をおく場所によって記録される波形が異なることを知った上で,先行研究と比較しやすいような基準部位を選ぶのがよいでしょう。心配ならば,分析時にいくつかの基準が選択できるように,複数の部位(A1, A2, 鼻尖,頭部外)から共通の基準を使って記録しておくことを薦めます。また,たくさんの電極をつけるならば,平均基準を使った分析も試してみましょう。
Q3. 両耳朶連結基準はよくないのですか?
両耳朶連結基準がよくないといわれる理由は2つあります。一つは,耳朶を基準にすることの問題です。前の質問への回答で述べたように,基準電極の近くでは電位が小さく記録されます(基準電極の活性化)。側頭部に大きな電位が予測されるときに耳朶を基準にすると,側頭部の電位を過小評価する可能性があります。ただし,この問題は耳朶よりもマストイドを基準にしたときに深刻です。前述のように,マストイドを基準部位とするのは薦められません。
もう一つは,左右部位を連結することの問題です。左右部位を連結する目的は,左右半球の電位差を検討するときに偏りがないように,左右の平均電位(脳中央部の電位の推定値)を基準にするためです。以前の脳波計では,左右の耳朶電極を物理的に連結させて記録することがありました。この方法には,いくつかの欠点があります。(1) 導線を通じて左右の電極間に電流が流れ,左右半球の電位差が小さくなってしまう,(2) 耳朶と電極間の抵抗が左右で異なっていると電位が中心ではなく左右にずれてしまう(左電極が外れて右電極だけで記録したとしても「両耳朶連結」とよばれることになる)。このような欠点は,物理的な連結をやめることで回避できます。前の質問への回答で述べたように,左右の基準を別々のチャネルで記録し,あとで基準を計算しなおせばよいのです。具体的には,次のようになります。まず,左耳朶(A1)を基準として脳波信号を記録し,同時に右耳朶(A2)の電極からも左耳朶(A1)を基準として記録しておきます。そして,分析時にすべての脳波データからA2で記録された電位の2分の1を引算すれば,結果的にA1-A2連結で記録したのと同じ波形が得られます。
結論として,物理的に連結しないのであれば両耳朶連結を基準にしても問題はありません。左右半球差を検討するのであれば,左耳朶(A1)ないし右耳朶(A2)を単独で基準とするよりも合理的です。もちろん,鼻尖を基準にする方法もありますが,先行研究と比較する上で都合がよければ,両耳朶連結を基準としてもよいでしょう。
Q4. 電極配置について,以前の10-20法と新しい10%法はどこが違いますか?
国際脳波・臨床神経生理学会連合(現・国際臨床神経生理学会連合)が国際標準として推奨する10-20法を,多チャンネル記録に対応するために1991年に拡張したのが10%法(拡張10-20法)です。違いは,正中線上の4箇所の部位名(AF, FC, CP, PO)を追加定義したことと,部位の命名に一貫性を持たせるために10-20法の4部位(図2の黒丸)の名称を変えたことです(T3/T4→T7/T8,T5/T6→P7/P8)。詳しい説明は,ERPの解説記事 (PDF) のFig. 2を見てください。
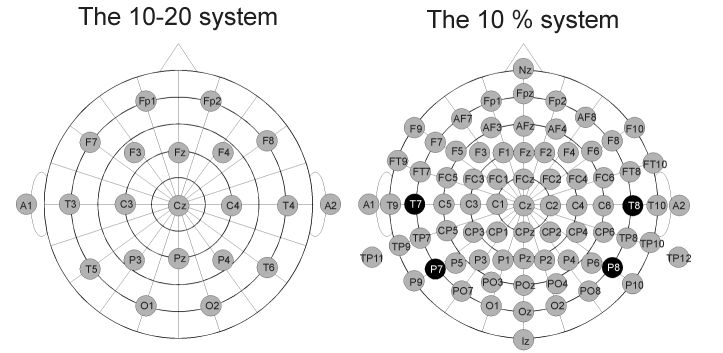
図2. 脳波電極配置法。
Q5. 電極帽を使うときに気をつけることは?
たくさんの電極を短時間で装着するのに便利なのが電極帽です。以前は,Electro-Cap International 社のエレクトロキャップ(Electro-Cap)だけでしたが,現在はいろいろなメーカーから販売されています。ElectroCapを使うときに気をつけるのは,説明書どおりにボディーハーネスをつけることです。そうしないと側頭部と後頭部の電極が上にずれます。胸にバンドを巻くのがいやなときは,専用の顎ひも(マジックテープで止める)も販売されています。熟練者が正しく装着すれば,電極位置は最大1cmくらいしかずれないことが報告されています(Blom, J.L., & Annevedt, M. 1982. Electroencephalography and Clinical Neurophysiology, 54, 591-594)。
もうひとつ気をつけたいことは,標準品のElectro-Capの電極はスズで出来ていることです。測定編Q1で述べたように,これは脳波記録には適していますが,ERP記録にはAg/AgCl電極の方が望ましいです。ただし,通常の脳波計で記録するときには(入力インピーダンスが高いので),どちらの電極を使っても波形はほとんど変わらないという報告もあります(Polich, J., & Lawson, D. 1985. American Journal of EEG technology, 25, 187-192)。Ag/AgCl電極がついたElectroCapは特注品で,価格は標準品の約3倍です(19 ch:19万円,32 ch:47万円程度)。セットになった耳朶用Ag/AgCl電極も販売されています。焼結タイプの電極なのでメンテナンスは楽ですが,標準のスズ電極よりも格段にもろい(硬いもの[たとえばニードル]で引っ掻くと崩れる)ので,装着するときや洗浄するときには注意が必要です。他のメーカーは,Ag/AgCl電極がついた電極帽をもっと安く販売しているようです(たとえば,Compumedics/NeuroScan社 Quik-Cap 32 ch:31万円,日本代理店 株式会社フィジオテック)。以上の値段は目安です。Quik-CapのAg/AgCl電極はElectroCapの電極よりも耐久性があります。また,専用の修理キットも市販されているので,自分でメンテナンスできます。普通のAg/AgCl電極と焼結タイプのAg/AgCl sintered電極がありますが,メーカーはやや高い後者を推奨しています。既製品のQuik-Capは,両耳(マストイド)用の電極が物理的に連結されています。これはやってはいけないことなので(測定編Q3参照),なぜかそうなっているのか分かりませんが,指定すれば独立したチャンネルに改造してくれます(7,500円程度)。納期はだいたい2ヶ月くらいだそうです。電極帽は,他にも数社から販売されています(たとえば,ドイツ EASYCAP社(旧 Falk Minow Service社)の EASY-CAP)。
材質の違う金属電極の間には電流が流れますから,スズ電極とAg/AgCl電極を混在させて使ってはいけません(生体内に電流が流れることになり,正常に記録できない)。また,同じAg/AgCl電極でもメーカーによって組成が異なりますから,使う電極は同じメーカーの製品で統一するのが無難です。
現在よく使われている3つの電極帽の比較と私の感想です(情報は多少古いかもしれません)。2006.8.11追加
| 名称 | Electrocap | Quikcap | Easycap |
| 販売会社 | Electro-Cap International (米) | NeuroScan (米) | EASYCAP (独) |
| 電極の材質 | 標準品はスズ(銀-塩化銀タイプも特注できる) | 銀-塩化銀(推奨は焼結型) | 焼結型の銀-塩化銀(直径約2 cmで中央に約1cmの穴があいたドーナツ型) |
| 電極の位置 | キャップの内側に固定。 | キャップの外側に固定。 | キャップの外側にリングアダプタでひとつずつ取りつける。電極位置を自分で変えられる。 |
| 電極の取付方法 | 先の尖っていないニードルで,手探りで髪の毛を掻き分け,頭皮をこすって,ゲルを注入する。ニードルの値段が高い。不良電極は外側からクイックインサート電極を使ってバイパスできる。 | Electrocapと同じ。ただし,インサート電極がないので,測定時に不良電極が出ても対処できない(実験後に電極を修理・交換できる)。 | ドーナツの穴から,綿棒などで目視によって髪の毛を掻き分け,頭皮をこする。ニードルなしのシリンジでゲルを注入。 |
| 電極の耐性 | スズ電極は丈夫だが,銀-塩化銀電極は表面がもろい。銀-塩化銀電極とリード線との接合部が弱い。 | 銀-塩化銀電極本体はElectrocapよりも丈夫だが,リード線との接合部が非常に弱い。 | 電極表面・接合部・リード線とも丈夫。少し重いのが欠点。 |
| 価格 | 標準品は安価だが,銀-塩化銀タイプの特注品は高い。 | 銀-塩化銀電極にするならElectrocapより安価。 | 銀-塩化銀電極ではもっとも安価。 |
| 推奨ゲル | Electro-Gel (薄褐色) 洗うときに水に溶けにくい。 | Quik-Gel (白色) 皮脂を溶かす成分が入っているようでインピーダンスが落ちやすい。 | Abralyt 2000(灰色) 研磨剤入り。 |
| キャップの材質とサイズ | 伸縮性はあまりない。電極とリード線がキャップの中にあるので,かぶり心地が悪い。日本人成人であれば,Mサイズ(54-58 cm,赤色,大半の女性と男性の一部)とLサイズ(58-62 cm,青色,男性の一部)を使う。ボディーハーネスまたはアゴヒモでとめる。アゴヒモのときは首が締めつけられる。洗浄後はやや乾きにくい。 | 3つのなかでもっとも伸縮性がある。アゴの先で止めるので,首が締めつけられずにかぶり心地がよい。サイズの種類は少なく,日本人成人であればMサイズ(54-62 cm)だけで十分。頭が小さい人はブカブカで電極と頭皮の距離が拡がってしまう。キャップの上から,頭部用のネット包帯をかぶるという方法もある。洗浄後は乾きにくい。 | 伸縮性はあまりないが,電極とリード線がキャップの外にあるので,かぶり心地がよい。キャップのサイズは2 cm刻みで豊富。日本人の成人であれば,女性は54 cmか56 cm,男性は56 cmか58 cm。60 cmは不要だが,52 cmはあってもよいかもしれない。ボディーハーネスまたはアゴヒモでとめる。専用のアゴヒモは使い勝手がわるい。洗浄後は電極を外すので,乾かしやすい。 |
| 総合評価 | 老舗なので安心できる。初心者向けといえる。 | かぶりやすさと高性能ゲルは評価できる。電極のもろさとサイズの種類の少なさがネック。 | 玄人好み。電極装着の仕方,電極位置の柔軟さ,キャップサイズの豊富さなど,他にない特長をもつ。最大の難点は,すべての電極がバラバラなので,装着時に電極とアンプの接続を間違えやすいこと。 |
Q6. ERPを記録するときのフィルタ設定はどうしたらいいですか?
どのERP成分に注目するかによってフィルタの設定は変わります。ゆっくりした電位の変化を除去する低周波遮断(ローカット)フィルタと,すばやい電位の変化を除去する高周波遮断(ハイカット)フィルタの2つにわけて説明します。
まず,ローカットフィルタですが,時定数(time constant: TC またはτ[タウ])であらわすこともあります。時定数とは,一定の入力信号の振幅が1/eにまで減衰する時間を示します(e は自然対数の底で 2.718…なので,0.367…)。いいかえると,一定の入力信号が約3分の1(37 %)の振幅になるまでの時間です。時定数は,遮断周波数(パワが1/2になる周波数)が1/(2πτ) Hzのローカットフィルタに相当します。もっと正確にいうと,減衰傾度が6dB/oct(周波数が2分の1になると振幅が2分の1になるスロープ)の順方向フィルタ(forward filter)です。脳波記録の標準は0.3 s(約 0.5 Hz)ですが,ERPでは緩やかな電位変化を検討することが多いので,3.2 s (約 0.05 Hz),5 s (約 0.03 Hz),10 s (約 0.016 Hz),16 s (約 0.01 Hz)といった長めの時定数(低めのローカットフィルタ)を設定します。脳波計によっては,直流増幅(direct current: DC,入力信号が減衰しない=時定数∞)ができるものもあります(NeuroScanなど)。時定数が長いと,発汗や皮膚電気活動の影響を受けやすい,一度振り切れてしまうと基線に戻りにくいといった測定上の難しさがあります。しかし,長い区間のERP波形を歪みなく記録するには,長い時定数や直流増幅が必要です。目安として,見たい現象の3倍の長さの時定数を使うことを薦めます。刺激が呈示されてから1秒間の波形を歪めずに記録するには,3秒の時定数を使えばいいことになります。下図に示すように,それ以上長い時定数を使っても波形はほとんど変わりません。(時定数の説明が間違っていたので訂正しました。2004.12.3)
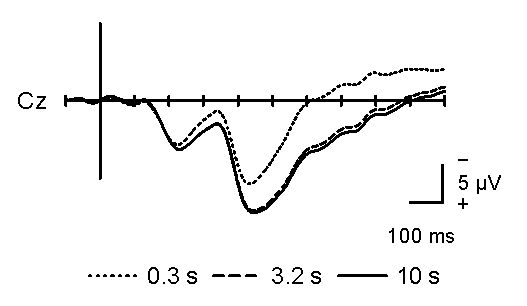
図3. ERP波形に及ぼす時定数の効果。視覚3刺激オドボール計数課題におけるターゲット(p = .125)に対する16名の総加算平均波形。中心部(Cz)における刺激呈示開始後1秒間の波形を示している。アナログ脳波計で記録時から時定数をかえて記録した。(両耳朶連結基準,ハイカットフィルタ30Hz,サンプリング周波数 200 Hz)。時定数が0.3 sのときは明らかに波形が歪んでいる(基線への戻りが早くなっている)。記録した区間の3倍以上の長さの時定数 3.2 sと10 sでは,波形にほとんど差がみられない。
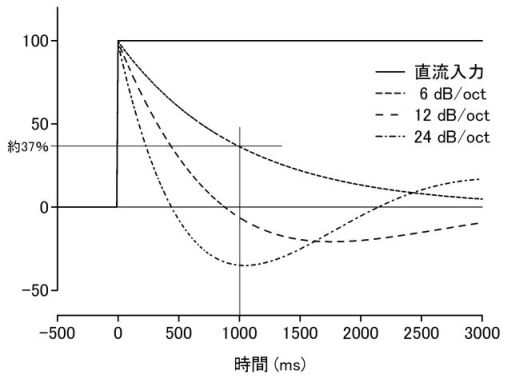
図4. 直流入力信号に及ぼすローカットデジタルフィルタの効果。遮断周波数が0.16 Hzでスロープが異なる順方向フィルタを適用した(BESA2000を使用)。時定数(この場合は1 s)の定義にあてはまるのは 6 dB/octのデジタルフィルタで,スロープが大きいと波形が歪む。
つぎに,ハイカットフィルタですが,2つの要因で決めます。一つは,見たい現象の持続時間です。潜時の短い初期成分を調べるには,高い周波数(60~100 Hz以上)のフィルタを設定する必要がありますが,P3(P300)のような緩やかな電位変化を対象にするならば,30 Hz程度のフィルタをかけても振幅が小さくなるといったことはありません。電灯線のノイズは東日本で50 Hz,西日本で60 Hzですので,それよりも低い周波数のハイカットフィルタをかけると電灯線ノイズの影響が減ります。ただし,ハイカットフィルタは分析時にデジタルフィルタとしてかけることもできるので,記録時には高めの周波数のフィルタをかけておくのがよいでしょう。もう一つの要因は,エイリアシング(aliasing)対策です。ERPを求めるには,波形をA/D変換して数値データにします。そのときの変換率(サンプリング周波数)の1/2以上の周波数の信号は原理的に記録できません(一つの波をあらわすのに最低2点が必要だから)。たとえば,1秒間に100回の割合でサンプリングしたときには,50 Hz以上の周波数は記録できないことになります。記録できないだけでなく,高い周波数の信号は,それより低い周波数の信号に混じってゴーストのようにあらわれてきます。これを防ぐために,サンプリング周波数の1/2以上の周波数帯域の信号は,A/D変換の前にハイカットフィルタをかけて取り除いておく必要があります。これをアンチエイリアシングフィルタといいます。実際は,サンプリング周波数の3分の1から4分の1の周波数のアンチエイリアシングフィルタを設定することが多いです(200 Hzサンプリングでは60 Hz程度,1000 Hzサンプリングでは300 Hz程度)。
なお,現在のデジタル脳波計では,設定したサンプリング周波数の1/3程度のアンチエイリアシングフィルタが自動的に設定されます。また,データはその脳波計がもつ最長の時定数で保存されます。そのため,分析時にフィルタ設定を自由に変えることができます。しかし,アナログ脳波計の出力をA/Dボードで取り込むときは,フィルタ設定を後で変更できないので,上記の注意事項にしたがって慎重に決定しましょう。
デジタル脳波計の場合,外部機器からの入力(DC入力)にも自動的にアンチエイリアシングフィルタがかかります。そのため,矩形波を入力しても,立ち上がり/立ち下がりが鈍い(なまった)波形になります。デジタル脳波計で矩形波をトリガとして使用するときは,トリガの立ち上がり時点が不明瞭になりやすいので気をつけましょう。
Q7. 短い時定数で記録したデータで長潜時成分を検討できますか?
短い時定数のままで分析することはあまり勧めません。Q6で述べたように,短い時定数では長潜時成分の形状が歪み,振幅が小さくなるからです。このような場合には,時定数の影響を加算平均波形上から計算によって取り除く方法があります。脳波計に含まれる時定数の回路が正しければ,厳密な数学的・電気的特性に従うので,時定数がない元の信号の状態,つまり,直流記録(DC)したときの波形を再現できるのです。図3で得られたデータを補正して,時定数の影響を取り除いた波形を図4に示しました。ご覧のように,きれいに補正できています。この方法は,短時定数の脳波計しか利用できない場合だけでなく,CNVやSPNなどの緩電位を10 s程度の時定数で記録するときにも役に立ちそうです(ただし,時定数を正確に知る必要がある)。今回の例では,10 sの時定数を使ったときでも,1秒間の加算平均区間の終わりになると,約 0.5 μV の時定数の影響が認められました。
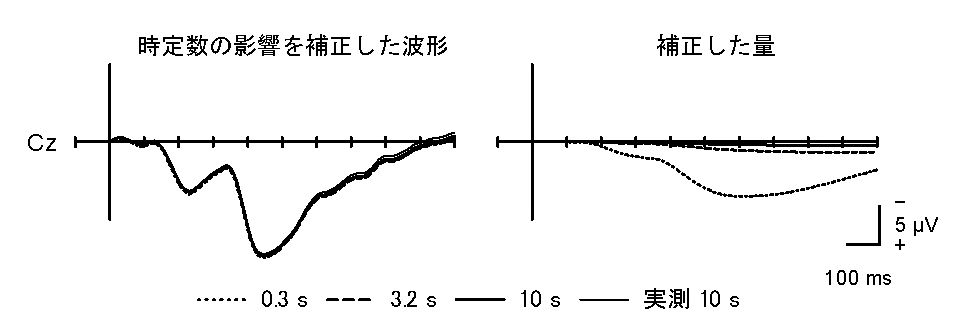
図5. 時定数の影響を補正したERP波形。図3のデータから,Elbert & Rockstroh (1980)の方法で計算して求めた (Elbert, T., & Rockstroh, B. 1980. Psychophysiology, 17, 504-505)。時点 t (ms) における時定数の影響は次の式で算出できる。 [(刺激オンセットから潜時 t までの区間の平均振幅)×t / 1000 ] / 時定数 (s)。たとえば,潜時500 msにおける時定数の影響は,0-500 ms 間の平均振幅に 0.5 ( = 500 ms /1000)をかけた値を時定数で割って求める。この例では,0.3 s のときの区間平均電位は 3.78 μVだったので,3.78 x 0.5 / 0.3 = 6.30 μV だけ,時定数のせいで波形がベースラインに戻っていることになる。同じ潜時における時定数10 sのときの影響は0.26 μVである。この補正値を連続的に算出して,実測値に加えていけば,直流(DC)記録したときと理論的に同じ波形が得られる。この図では,便宜的に測定値を刺激前ベースラインに揃えてから補正を行っているが,厳密にはこの方法は不適切である(下記参照)。
しかし,この方法には使用上の注意と限界があることが指摘されています (Ruchkin, D. S. (1993). AC-to-DC inverse filtering of event-related potentials. In W. C. McCallum, & S. H. Curry (Eds.), Slow potential changes in the human brain (pp. 91-97). New York: Plenum Press)。(1) 通常の時定数の回路(一組のコンデンサと抵抗を使う)にしか適用できない。(2) ベースラインを正しく補正しないと歪みが出る。(3) 測定誤差の影響は時間とともに蓄積していくので,無制限に長い区間は変換できない。このため,次の方法が提案されています。(1) 定常誤差を除去するため,入力をショート(インスト)させたときに出力(測定値)がゼロになるように校正する(これは測定後に計算で行ってもよい)。(2) 刺激前ベースラインは時定数の影響を補正した後に行う(前に行うと定常誤差の原因となる)。(3) できるだけ長い時定数を使う(時定数が長いほど,測定誤差が補正に及ぼす影響が小さくなる)。使い方に注意すれば,緩電位の研究に有用な方法だといえます。ただし,市販の脳波計であっても,チャンネル間で時定数にかなり誤差があるという報告もあり,正確な補正を行うには時定数を自分で測定する必要があります (Joyce, C. A., et al., 2002. Psychophysiology, 39, 633-640). 短い矩形波パルスから時定数を計測する方法についても述べられている)。(2004.12.16追加)
Q8. サンプリング周波数はどのくらいにしたらいいですか?
サンプリング周波数が高いと,(1) 波形をなめらかに再現できる,(2) 時間的分解能(潜時の測定精度)が高くなるといった利点があります。その反面,データ量が多くなり,計算や分析に時間がかかるようになり,保存に困るといった欠点もあります。刺激の呈示後1秒間くらいを検討するときは,最低 200 Hzで記録しておけば,十分に波形を再現できます。この場合,サンプリング間隔は5 msなので,潜時のよみとり精度は5 ms単位になります(100 ms,105 ms,110 ms,…)。数 msの潜時差を検討しようとする場合には,もう少し高いサンプリング周波数(250 Hz, 500 Hz, 1000 Hzなど)で記録するのが妥当です。
Q9. ERPの測定には,どのくらい試行数がいりますか?
加算平均法は,信号(事象に時間的に関連した脳波)をノイズ(事象に時間的に関連しない脳波)から分離する方法ですから,両者の振幅比によって有効な加算平均回数が決まります。ノイズに対して信号が大きいほど,少ない加算平均回数で波形を観察することができます。P3のような10μVを超える大きな電位は,20回程度の加算平均で安定して記録できます(Cohen, J. & Polich, J. 1997. International Journal of Psychophysiology, 325, 249-255)。N1やミスマッチ陰性電位(mismatch negativity: MMN)といった数μVの電位については60回くらいの加算平均が一般的です。実際の実験では,まばたきや眼球運動,筋電位など,脳波以外のノイズ(アーチファクト)が混入しますので,それ以上の試行数が必要です。目安としては,最低加算平均回数の約2倍の試行を用意しておけば安心です。試行数をあまり増やすと被験者が疲労し,実験の最初と最後でERP波形が変わる可能性がありますので,適当な試行数で終了するようにしてください。※2020年現在では,信頼できる波形を得るために,試行数は少ないよりも多い方がよいとされています。
Q10. どのくらいの時間を記録したらよいでしょうか?
ERPを記録するときは,実験中の脳波をすべて保存しておく場合と,加算平均に必要な事象の前後の区間のみを保存しておく場合があります。後者は,データ量が少なくてすむという利点がありますが,実験後に別の観点で分析したいとき(たとえば,事象の前の活動に条件差がなかったかを確認したいときなど)に不便です。また,保存した波形にデジタルフィルタをかけるときは,区間が短いと歪みが大きくなります。オンラインで加算するといった目的がないかぎりは,実験中の脳波データはすべて保存しておくのがよいでしょう。
Q11. ベースラインはどのくらいの長さがいいでしょうか?
ベースラインには,2つの意義があります。一つは,振幅測定のゼロ点になることです。加算平均波形の各データポイントから,ベースライン区間の平均電位を引算することで,ベースライン調整をします。ベースラインの長さは,覚醒時に高振幅で現われることがある脳波(アルファ波)の1周期分にあたる 100 msは必要だといわれています。これより短いと,アルファ波の位相によってベースラインが変動することになります。ベースラインのもう一つの意義は,加算平均後のノイズの程度を示すことです。事象が生じる前には何も起こってないと考えると,ベースライン区間にあらわれる電位変化はノイズだといえます。事象の生起後にも同程度のノイズが入っている(ベースライン区間の振れと同程度の振れはノイズの可能性がある)と仮定して,波形データを解釈するのが合理的です。
よく使われるのは100 msのベースラインですが,私は1秒以上の区間を検討するときは200 msのベースラインを使うことがあります。(1) ノイズの程度が分かりやすくなる,(2) ベースライン区間の電位の傾きから,事象に対する予期を反映した陰性電位が出ているかどうかを簡易に検討できる,というのがその理由です。
Q12. ERPを安価で測定するためのシステムはありますか?
脳波計と汎用PCがあればERPの測定はできます。最近では,デジタル脳波計が普及してきましたが,これは安いものでも3~400万円します。アナログ脳波計であれば,実習用としておいてある心理学教室は多いですし,中古品や廃棄処分になった物品を安価で手に入れることもできるでしょう。ただし,工業用や動物実験用のアンプを使ってはいけません。感電事故を起こす危険があります。必ず人間用に設計されたアンプ・脳波計を使ってください。
アナログ脳波計の外部出力をパーソナルコンピュータにさしたアナログ/デジタル(A/D)変換ボード(10万円程度で購入できます)につなぐことで,脳波信号をデジタル化(数値化)します。A/D変換ボードを制御するプログラムは,ボードに付属のドライバを利用して,個人でも作成可能ですが,市販の測定ソフトウェアを購入する方が簡便です。数社から販売されており,定価は100~150万円程度です。例えば,シグナルベーシックライト(メディカルトライシステム),BIMUTAS II,EPLYZER II(キッセイコムテック社)などがあります。また,一般科学計測用のソフトウェア(ナショナルインスツルメンツ社LabVIEWなど)を使うこともできるでしょう。
A/Dボードはできるかぎり同時サンプリング機能がついたものを使います。A/Dボードは1チャネルずつスキャンしてデータを取り込んでいくので,チャネルによって取り込みタイミングにわずかな時間差が生じます(1-10μs/ch,32 chで0.03-0.3 ms 程度)。サンプリング周波数が200 Hz(5 ms/point)くらいであれば無視できますが,1000 Hz(1 ms/point)になると影響が出てきます。同時サンプリングボードを別売しているメーカーもあるので調べてみてください(たとえば,CONTEC社のATSS-16)。
Q13. 安価な刺激装置はありませんか?
専用の刺激装置はたくさん発売されていますが,2~300万円以上します。安価に自作できる視覚刺激装置として,発光ダイオード(light emitting diode: LED)があります。赤・白・黄・緑・青などの色があり,従来の円形だけでなく,面状のものもあります。また,数字表示用の「セブン-セグメント」とよばれるLEDを用いれば,刺激の種類を豊富にできます。コンピュータやテレビに使われるブラウン管(cathode-ray tube: CRT)ディスプレイは1画面を描くのに10~20ミリ秒かかりますが,LEDは瞬時に点灯できるので,正確に時間制御ができます。
刺激提示ソフトウェアもだいぶ性能がよくなってきました。私の研究室では Millisecond Software社の Inquisit を使っています。質問紙なども同じプログラム上で測定できるので便利です。
可能なかぎり,トリガとCRT上の刺激提示タイミングのズレをフォトセンサで調べておいてください。実際,Inquisit 3.0は,Windows XP上で走らせるときは正確に時間制御できましたが,Windows 7上では数フレームの遅れが生じました。この問題は Inquisit 4.0や5.0では修正されていますが,自分が使っているシステムの時間精度を正確に知っておくことは大切です。Windows 10でHDMI経由で提示すると,試行ごとに時間のズレがばらつくこともあります。
通販で買えるフォトセンサの例として,浜松ホトニクスのSiフォトダイオード(S1787-04)があります(1個350円,2020年1月21日現在)。フォトダイオードは小さな太陽電池なので,光を当てると300 mV程度の電圧が生じます。そのまま外部入力から記録できます。CRTではリフレッシュレートに合わせてパルス状の光が記録できますが,液晶ディスプレイでは光量が緩やかに変化して立ち上がり,刺激提示中はずっと点灯しているのが分かります。
聴覚刺激は,Windowsで動く音声編集ソフトウェアを用いて作ると便利です。私は,Cool Edit 96 (Syntrillium Software Corporation; 現在はAdobe社に吸収)Audacity を使っています(2020年1月21日追記)。ステレオの左右チャンネル(L/R)に,刺激音とトリガをそれぞれ編集して入れることで,ERP測定用に使えます。WAVファイルとして保存したものをWindowsプログラム(Visual Basic等)で呈示します。ただし,PCのライン出力にはノイズがのりますので,イヤホンを使うときは少し耳障りです(スピーカ呈示ではそれほど気にならない)。そのような場合は,WAVファイルを一度CD-Rに記録して,オーディオ用のCDプレイヤで再生するとうまくいきます。A/Dボードの入力レンジによっては,小型アンプやレベル検出器(入力信号があるレベルを超えると一定の電圧を出力する装置)が必要になることもありますが,これらは千円ほどで自作できます(拙著『心理学のための事象関連電位ガイドブック』(p. 68)に回路を載せています)。CD-Rと携帯型CDプレイヤを組み合わせることで,実験室外でのERP測定が可能になります。この方法の欠点は音圧の調整が難しいことですが,P3(P300)などの後期ERPを調べるのであればそれほど問題になりません。
統計分析編
Q1. 頭皮上分布の差の検定はどのようにするのですか?
条件間の振幅の絶対値を除去した値で分散分析を行います。以下の式のように,被験者ごとのそれぞれの部位における振幅実測値を,ベクトル長(すべての部位の振幅値の二乗和にルートをかけたもの。全被験者の平均値を使って各条件について一つだけ求める)で基準化した値を使って分散分析を行います。この分析で,条件×部位の交互作用が有意になったときに,頭皮上分布に差があると判定します。詳細は,資料(PDF)を参照してください (2005.11.28 図を訂正しました)。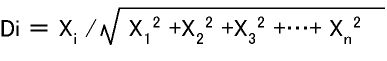
(Di: 基準化した振幅値,Xi: 部位iにおける振幅の実測値,n: 部位数)
しかし,最近では,この方法は使わない方がよいという提案もなされています (Urbach, T. P., & Kutas, M. 2002. Psychophysiology, 39, 791-808)。電位の頭皮上分布の違いが脳内の電位発生源の空間配置の違いに一対一で対応しているわけではないので,この方法は概念的に適切とはいえず,また,ノイズ(特にベースラインレベルの違いや他の電位の重畳)による影響を受けやすいので,実践的にも問題があるというのがその理由です。ベクトル長で基準化して頭皮上分布の差を検討するときは,「なぜそうするのが妥当なのか」の説明が求められるようになっています。
Q2. 通常の分散分析の自由度修正と多変量分散分析とはどちらがよいですか?
ERPの実験では,多くの部位から同時に記録したデータを被験者内要因(繰り返し測度)として分散分析を行います。隣り合う部位のデータが互いに関連している(独立でない)ことは容易に想像できます。水準が2つしかなく(例えば,右半球/左半球),その間に相関があることは,分散分析では問題ありません(これは,対応のあるt 検定と同じです)。しかし,3つ以上の水準があるときは注意が必要です。分散分析では,各水準がその要因の効果に等しく貢献していることを前提にしています。そのため,任意に組み合わせた2つの水準間の相関(共分散)は等しくなるはずです。しかし,実際には,このようなケースはまれです。たとえば,前頭部(Fz),中心部(Cz),頭頂部(Pz)の3部位から記録した振幅を比較すると,距離が近いFzとCzの相関は,距離が遠いFzとPzの相関よりも高くなると予想できます。つまり,分散分析の前提条件が崩れているわけです。
もう少し詳しく説明しましょう。もし,すべての水準の分散が等しく,かつ,すべての水準の組み合わせで相関(共分散)が等しければ(これを複合対称性 compound symmetry という),分散分析の前提が満たされます。しかし,これは大変厳しく,分散分析の必要条件ではありません(十分条件です)。分散分析の必要十分条件は,相関があると考えられる(つまり,被験者内要因の)すべての水準対の「差」の分散が等しいことだとされています (Huynh, H. & Feldt, L. S. 1970. Journal of the American Statistical Association, 65, 1582-1589; 小牧純爾, 1995. データ分析法要説, ナカニシヤ出版 )。この条件を,球面性の仮定(sphericity assumption)と呼ぶことがあります。上記の例では,FzとCzの振幅値の差の分散と,FzとPzの振幅値の差の分散が等しければ,球面性の仮定が守られているといえますが,実際にはほとんどありえません(距離が離れた方が振幅差が大きく,分散も大きくなる)。しかも,球面性の仮定の数は,繰り返し測度の要因数が増えるほど増えます(要因数をTとすると 2T-1で,交互作用を検定するための仮定が増える;Vasey, M. W. & Thayer, J. F. 1987. Psychophysiology, 24, 479-486)。他の研究分野では,まず球面性の検定をして,それが有意でなければ,通常の分散分析を利用するという方法が紹介されていますが,ERPのほとんどの研究では,繰り返し測度が2要因以上(たとえば,条件と部位,刺激と部位)なので,検定をしなくても,球面性の仮定が破られていると考えるのが現実的です。
このような球面性の仮定を破ったデータに,通常の分散分析を行うと,タイプⅠエラー(本当は差がないのに差があると判定するエラー)が大きくなります。そこで,(1) ε(イプシロン)という係数によって自由度を調整してから有意性の検定を行う,(2) 球面性の仮定を必要としない多変量分散分析(multivariate analysis of variance: MANOVA)を行う,のいずれかの方法をとります。
統計学的にはMANOVAの方が優れています。しかし,MANOVAは,サンプルサイズ(被験者数)が水準数よりも十分に大きくないと,検出力が高くなりません。サンプルサイズが水準数より20以上大きいときは,MANOVAの方が検出力が高く,サンプルサイズが水準数より6程度しか大きくないときは,調整自由度を用いたANOVAの方が検出力が高いといわれています(Davidson, 1972, cited in Vasey, M. W. & Thayer, J. F. 1987. Psychophysiology, 24, 479-486)。MANOVAは,サンプルサイズが水準数より少ないと(自由度より1以上大きくないと)と計算できません。たとえば,条件(3水準)×左右半球(2水準)×部位(8水準)の繰り返し測度の分析をするときは,最低でも15名の被験者のデータがないと3要因の交互作用の値を計算できません(自由度 (3-1)×(2-1)×(8-1)=14よりも1以上大きいときに計算できる)。MANOVAの検出力を高めるためには,実際はこれよりも十分に大きいサンプル(30名程度)が必要だといえます。ERPの実験では,被験者の数が少ない(10~20名)ことが多いので,調整自由度を用いたANOVAが今でも使われています。
εの算出には,Greenhouse-GeisserとHuynh-Feldtの方法がよく用いられます。G-G法のεは,εが小さいとき(0.5程度かそれ以下)には適しているが,サンプルサイズが少なくεが1に近い(0.75程度かそれ以上)ときには自由度を小さく調整しすぎる(有意性の判定が厳しくなりすぎる)というバイアスをもっています(Huynh, H. & Feldt, L. S. 1976. Journal of Educational Statistics, 1, 69-82)。H-F法のεは,G-G法のεがもつこのようなバイアスを,サンプルサイズと水準数を使って修正したものです。H-F法のεはG-G法のεよりも大きめに計算されます。H-F法のεは1を超えることがありますが,その場合は自由度の調整は行いません。どちらの方法を使うのが望ましいといった明確な指針はないようですが,サンプルサイズが十分に大きいときはG-G法を,サンプルサイズが小さいとき(目安として10名前後,水準数の2倍程度)はH-F法を使うことが多いようです。一つの分析のなかでG-G法とH-F法をεの値によって使い分けることはしないので,被験者の数によってどちらの方法を使うかをあらかじめ決めておくのがよいでしょう。なお,サンプルサイズが大きくなると,G-G法とH-F法のεの差は小さくなるので,サンプルサイズが大きいときにH-F法を用いても問題ありません。結果には,調整前の自由度,自由度調整後に得られたp値,およびεを記載します。
MANOVAを使った場合にも,最終的には,(近似的に算出される)F値を検定し,その結果を記載することになるので,見た目はあまり変わりません(自由度は変わります)。統計パッケージでMANOVAを行うと,いくつかの統計量が算出されます。SASの場合は,Wilks’ lamda,Pillai’s trace,Hotelling-Lawley trace,Roy’s Greatest Rootの4種類です。これらの値は,それぞれ近似的に,ある自由度を持ったF値に変換され,検定に使われます。これらの統計量に基づいて計算したF値と自由度が同じになるとは限りません。どの方法が優れているとは一概にはいえないようですが,心理学のデータ(特にサンプルサイズが比較的少ない場合)には,Pillai’s trace (Pillai-Bartlett traceとも呼ぶ,記号 V)が推奨されています(Olson, C. L. 1976. Psychological Bulletin, 83, 579-586)。共分散行列の等質性の仮定からの逸脱に強く,検出力も高いと考えられるのが,その理由だそうです。心理生理学分野でも,この統計量が推奨されています(Keselman, H. J. 1998. Psychophysiology, 35, 470-478 [DOI][PDF])。Olson (1976)は,心理学の論文では,Wilks’ lamda(とその近似F値を求めるRaoの方法)が用いられることが多いと述べていますが,一般には Pillai’s trace の方が優れているらしいです。なお,MANOVAを行うときは,どの統計量に基づいて近似F値を求めたかを方法に明記する必要があります。
追加説明:MANOVAで近似F値と自由度が4つの基準で異なるのは,参加者間変数が3水準以上のときです。参加者間変数がないときや2水準のときは,どの方法を用いても変わりません(Keselman, H. J., Algina, J., & Kowalchuk, R. K. 2001. British Journal of Mathematical and Statistical Psychology, 54, 1-20)。従って,後者の場合では近似F値を求める方法を記載する必要はありません。参加者間変数がないとき(すべて参加者内計画のとき)のMANOVAでは,仮説の自由度は,通常のANOVAで計算される自由度(例:1要因のとき K-1,Kは水準数)と一致し,誤差の自由度は,参加者数から仮説の自由度を引いたものになります。(2006.6.23追加)
私には統計学の専門知識がないので,経験的なことしか分かりませんが,現在の心理生理学では,以上述べたような分析でほとんど通用します。説明に間違いがあれば,ご指摘いただけると幸いです。
ちなみに,「Huynh-Feldt」の読み方ですが,「ホイン-フェルト」や「ヒュン-フェルト」ではなくて,「フィン-フェルト」が正しいと思われます。人名の本当の発音は本人にきかないと分からないのですが,(1) Huynh氏(姓も名もHuynhで,Huynh Huynh というらしい)はサイゴン大学(ベトナム)の統計学の教授であること(Huynh, H. & Feldt, L. S. 1970. Journal of the American Statistical Association, 65, 1582-1589),(2) ベトナム人のHuynhは「フィン」と日本語表記されること(外国人物レファレンス事典20世紀 2E-K,日外アソシエーツ,p. 543),を考慮すると,「フィン-フェルト」が正解に近いといえます。確かに,「Huy-」は「ホイ-」と読まれることもありますが(たとえば Huygens[ホイヘンス:オランダの物理学者]),科学分野の外国人がすべて西洋人とはかぎりません。
Geminiに聞いてみると,”Hwin-Felt” or “Hwihn-Felt” に近いとのことでした。ちなみに “Green-house Guy-ser” とのこと (2025.6.26追加)。
Q3. 効果量(effect size)とは何ですか?
最近は,論文で結果を報告するときに,p値だけでなく,効果量(効果の大きさ)を報告することが推奨されています(たとえば,APA Publication Manual, 5th ed., pp. 25-26)。統計の入門書にはあまり書かれていないので,難しいと避けてしまいがちです。特に,メタ分析やパワー分析と一緒にすると混乱します。しかし,効果量そのものは,そんなに難しい概念ではありません。
通常行う統計検定は,帰無仮説(たとえば,両群の平均値に差がない)を棄却するという手続きで行います。その結果,あらかじめ決めておいた有意水準よりも低いp値が得られると「有意である」と判定します。しかし,この結果が意味するのは,「差がないというよりも,あると考えた方が合理的だ」ということだけです。p値が0.04でも0.00001でも,言えるのは同じことです。p値は,効果の大きさを示すものではなく,サンプルサイズによって変わるものです。10人のデータでは有意でないが,1000人のデータでは有意であることは多々あります。10人のときに有意でなかったのは,その統計手法に十分なパワー(検出力)がなかったからです(このあたりは,橘敏明, 1986. 医学・教育学・心理学にみられる統計的検定の誤用と弊害, 医療図書出版 [絶版]に詳しい)。
追加説明:これまで「サンプル数」という語を慣用的に使ってきましたが,正確ではないので「サンプルサイズ」に置き換えました。統計学では,一つのサンプル(=母集団の部分集合)に含まれるデータ数のことです。日常語の「標本」は,生物や鉱物の見本の意味で使われますが,これは英語ではspecimenといいます。サンプルには見本・試供品の意味もあります。そのため,個人や個体を表すイメージがあり,サンプル数と言ってしまうのでしょう。たくさんのサンプル(異なる研究における参加者集団)を実際に扱うメタ分析が普及してきたので,気をつけて使いたいと思います。(2018.8.7追加)
統計検定における有意差の解釈は, 2変量の積率相関(ピアソンの積率相関係数 r)の検定(ゼロか否か)を例にすると分かりやすいです。たとえば,2変量A,B間の相関係数が r = 0.2だったとします(ちなみに,1を超えない数値については小数点前の0を省略するのがAPA の規定です [Publication Manual, 5th ed., p. 128]。しかし,雑誌によっては省略しないこともあります)。この値が10人のデータから得られた場合には,有意水準を両側5%にすると有意になりません(自由度10-2 = 8,臨界値 0.632,p = 0.58)。しかし,1000人のデータから得られた場合には有意です(自由度1000-2=998,臨界値 0.062, p < 0.00001)。また,逆算すると,98人のデータを集めれば,この相関係数を“有意にする”ことができます(自由度96,臨界値0.199, p = 0.048)。しかし,有意になったからといって,また,p値がいくら大きくても,相関係数そのものは変化しないので,2変量A,Bの関係が強くなるというわけではありません。つまり,この有意性検定でいえるのは,「相関係数はゼロではない(と考えた方が合理的だ)」ということだけです。 r = 0.2という相関係数は,サンプルサイズやp値に関係なく,それほど大きくないのです。
以上の理屈は「あたりまえ」のように思えます。しかし,t検定や分散分析になると,この理屈を忘れてしまい,p値の大小が“効果の大きさ”を表わしているかのように錯覚しがちです。統計検定で扱うのは「差(効果)があるかないか」という二者択一の判断であって,差(効果)の大きさではないということを再確認しておきましょう。
そこで,(サンプルサイズに左右される)p値とは別に,(サンプルサイズに左右されない)効果の大きさを表現する必要が出てきます。t検定や分散分析で効果量を示すには,まず平均値と分散(標準偏差)を示すことが肝要です。スペースなどの関係で,これらの記述統計値を示さずに p値だけを報告している論文をときどき見かけますが,やめた方がいいでしょう。
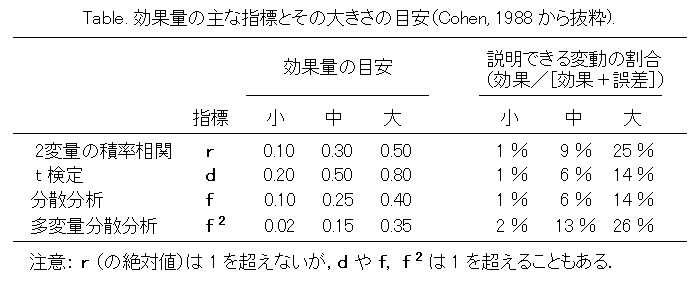
平均値と分散を見れば,その実験での効果の大きさはおよそ分かるのですが,異なる実験間で比較できるように標準化しておいた方が好都合です。効果量の指標とその算出方法について,Cohen, J. (1988) の Statistical power analysis for the behavioral sciences, 2nd ed.) . Lawrence Erlbaum. を参考に説明します。
2変量の積率相関における効果量の指標は,ピアソンの積率相関係数 r (の絶対値)をそのまま使います。
t検定における効果量の指標は,d = 2群間の平均値の差/2群をプールした標準偏差(=それぞれの群のデータの分散を求め,それを平均したものにルートをかける[サンプルサイズが異なっているときは重みづける]) です。日本語の統計教科書によく出ているのは,対応のないt検定の例ですが,対応のあるt検定でも,d の式は同じです。つまり,測定値に対応がある場合でも,対応がない場合のように扱い,2条件をプールした標準偏差を求めて,d を計算すればよいのです。各群でサンプルサイズが同じ(n1=n2=n)であれば,対応のないt検定(等分散を仮定)のt値を使って,d = t*√(2/n)と表現できます(データに対応がある場合も同じ)。人数が違っていれば,d = t*√(1/n1+1/n2)として求めます(Cumming, 2012, p. 289)。
対応のあるデータで直接dを求めるときは,条件間の平均値の差を各条件の標準偏差の二乗(不偏分散)の平均値の平方根√((s1^2 + s2^2)/2)で割ります(Cumming, 2012)。このようにして求められるdは,上述の対応のないt検定のt値を使って求めた値とまったく同じです(松田いづみ先生による指摘)。Lakens (2013) は, Cumming (2012)を引用しながら,分母を標準偏差の平均値(s1+s2)/2 としたものをdavと呼んでいますが,これは対応のないt検定のt値を使って求めた値とは異なります。(2018.8.6追加; 2020.8.23訂正)
対応がある検定では,対応がない検定に比べて,有意差が出やすく(=検出力が高く)なります。これは効果量 d が大きくなるからではありません。効果量は同じですが,対応があれば,その情報(測定値間の相関関係)を利用して検出力を高められるということです。効果量と有意性検定は直接関係しないことを再確認しましょう。
追加説明1: 標準偏差を求めるときに2群をプールするのがよいかどうかは状況に依存します。統制群(の母集団)と実験群(の母集団)が等分散であるといえれば,統制群の標本と実験群の標本をプールすることで,より信頼できる分散・標準偏差を求められます。しかし,両群の母集団の分散が違っていれば(たとえば,実験変数の効果が個人によって異なっていれば),実験群をプールすることで,分散を誤って推定してしまうことになります。このような場合には,統制群(未処置群)の標本だけを使って効果量 d を求めた方が,「自然に生じるばらつきと比べて,実験変数の効果がどのくらい大きいか」を表わすことになるため,より合理的です。このあたりは,統計の教科書によっても記載にぶれがあるようです。(2011.6.8追加)。統制群のばらつきだけを利用する効果量が GlassのΔです。(2018.8.6追加)
追加説明2:対応のあるt検定の効果量は,平均値の差を「差分値の標準偏差」で割って求める場合もあります(dz)。こうすると統計検定とは一貫しますが,参加者内デザインと参加者間デザインで,効果量の意味が変わってしまいます。dz を使わないほうがよいと主張するのは,Dunlap et al. (1996)です。ただ,絶対値ではなく変化量(差分値)にしか興味がない場面では,絶対値の標準偏差ではなく,差分値の標準偏差を基準にして平均値の差の大きさを表現した方が素直です。効果量を求めるソフトウェア(RやG*Power)では,このdzをdの値に入力することがあります。Cumming (2014)が述べるように,Cohen’s d を一般的な名称として使い,その計算方法を論文に記載するのがよいのでしょう。(2017.11.15追加)
追加説明3:dz は,対応のあるt検定のtの値を使って t/√n の式で求められます(Lakens, 2013の(7)式)。また,対応のある条件間の相関係数 r を使うと,d = dz / √(2(1-r)) と変換できます。r = .5 のときは d = dzですが,たいていは r > .5なので,d は dzよりも小さくなります。Nakagawa & Cuthill (2007)では,対応のある場合のHedgesの補正の式がCumming (2012)とは異なっています。Hedges (1981)によると,補正係数はdfによって決まるので,Cummingのほうが正しいようです。Cumming (2012, p. 298)に従って,効果量dの計算をまとめると,以下のようになります。(2018.8.6追加)
1. 固定値(μ0)との比較 df = N – 1, d = (M – μ0)/s
2. 対応のないt検定 df = N1 + N2 -2, d = (M2 – M1)/sp
sp はプールした標準偏差(分母をN1 + N2 -2として計算するもの)
3. 対応のあるt検定 df = N – 1, d = (M2 – M1)/sav
sav は2条件の不偏分散を平均した値の平方根
このようにして求めたdを不偏推定値 dunb(ディー・アンビー; Cumming, 2012による)にするには,d に 補正係数 1 – (3/(4df – 1)) をかける。
例:d が 0.5 とすると,
対応なし 10人ずつ:dunb = (1- (3/(4*(10+10-2) – 1)) * 0.5 = 0.957 * 0.5 = 0.479
対応あり 10人 :dunb = (1- (3/(4*(10-1) – 1)) * 0.5 = 0.914 * 0.5 = 0.457
※この不偏推定値 dunbを Hedges’ g と呼ぶこともあります(Borenstein et al., 2013の第4章)。しかし,上記の対応のないt検定のdの意味で使う人もいます(Cumming, 2012)。
Borenstein, M., Hedges, L. V., Higgins, J. P. T., & Rothstein, H. R. (2009). Introduction to Meta-Analysis. Chichester, England: Wiley.
Cumming, G. (2012). Understanding the new statistics: Effect sizes, confidence intervals, and meta-Analysis. New York, NY: Routledge.
Cumming, G. (2014). The new statistics: Why and how. Psychological Science, 25, 7-29.
Dunlap, W. P., et al. (1996). Meta-analysis of experiments with matched groups or repeated measures designs. Psychological Methods, 1, 170-177.
Hedges, L. V. (1981). Distribution theory for Glass’s estimator of effect size and related estimators. Journal of Educational Statistics, 6, 107-128.
Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: a practical primer for t-tests and ANOVAs., Frontiers in Psychology, 4:863.
Nakagawa, S., & Cuthill, I. C. (2007). Effect size, confidence interval and statistical significance: A practical guide for biologists. Biological Reviews, 82, 591-605.
t検定の効果量の指標として, rを使うことがあります。
r = √[t^2 / (t^2 + t検定の自由度)] *対応がある分析でもない分析でも,対応のないt検定のときの値を使う。
という公式で求められます。このときの r は,2条件のデータ間の相関ではないことに注意してください。点双列相関(point biserial correlation)とよばれるものです。たとえば,3人の参加者が条件A,Bの両方を行い,条件Aではそれぞれ 4,5,6,条件Bではそれぞれ 2,7,3 というデータが得られたとします。このとき,条件Aを0,条件Bを1という名義尺度にし,(4, 5, 6, 2, 7, 3) と (1, 1, 1, 0, 0, 0) というデータの組から積率相関を求めたのが,ここでいう r です。計算すると,r = .293になります。この計算法から, データに対応があるかないかは r と関係していないことが分かるでしょう。ちなみに,d を計算すると,d = (5-4)/2 = 0.5 になります。
このデータを対応のない t 検定で分析すると,t = 0.612, 自由度 = 4 です。公式に従うと,r = √[0.6122/(0.6122+4)] = √[0.375/(0.375+4)] = 0.293 となり,データから直接求めた値と一致します。ちなみに,対応のある t 検定で分析したときは,t = 0.655, 自由度 = 2 です。 r = √[0.6552/(0.6552+4)] = √[0.429/(0.429+2)] = 0.420 となり,一致しません。この公式が対応のあるなしにかかわらず使えると書いてある文献もありますが(例: Field, A. (2009). Discovering Statistics Using SPSS (3rd. ed). Sage),それは間違いです (Dunlap, W. P., et al. (1996). Meta-analysis of experiments with matched groups or repeated measures designs. Psychological Methods, 1, 170-177)。
なぜ間違いと言えるか? それは,効果量には,黄金律といえるスタンダードな求め方(平均と標準偏差から求める方法と点双列相関を求める方法)があるからです。
r = d /√(d^2 + 4) (Cohen, 1988, p. 23) または d = √[4r^2 / (1-r^2)] (Dunlap et al., 1996, Appendix B) *この2つは同じ式です。
近似式として,r = 0.5d (-0.41 <= d <= +0.41 のとき)(Cortina & Nouri, 2001)
のように d と r の変換式を載せている文献もありますが,これはサンプルサイズが十分に大きい([n-1] / n を1で近似できる)という仮定に基づいた式です(Dunlap et al., 1996; 松田いづみ先生にご指摘いただきました)。他人のデータをメタ分析するのではなく,手持ちのデータを報告したいのであれば,変換式は使わず,データから直接計算することを勧めます。その方が簡単です。スタンダードな方法で求めるときにも,暗黙の仮定(2群のデータは正規分布していて等分散であり,ランダムサンプリングされている等)は存在します。しかし,そのあたりを気にしだすと,際限がありません。
なお,点双列相関によって表わした効果量の大きさは,通常の積率相関係数のときと同じように解釈できます。たとえば,上表では,「説明できる変動の割合」として r^2 の値を示しています。t検定の効果量を r で表わしたときも,r^2 には同じ意味があります。つまり,全データ分散のどのくらいの割合が,どちらの群・条件に属するかによって決まるかを示しています。(t検定の効果量についての説明:2011.3.24追加,3.25修正)
3水準以上の分散分析でも,2群ごとに組み合わせて比較するときは,この d を使うことができます。その場合,どのように標準偏差をプールするかが問題になりますが,さまざまなケースについての算出方法が,Cortina, J. M., & Nouri, H. (2001). Effect size for ANOVA designs. Sage. に載っています。
効果量の目安は,Cohen(1988)が,行動科学における慣習的な数値として提案しているもので,これに従って,効果量が大きいか小さいかを操作的に定義します(pp. 12-13)。慣習(convention)というのは,たとえば,通常の統計検定で有意水準を5%とするのと同じように,「理論的な根拠はないが,それなりに合理的で理解できる」という意味です。f^2 の効果の大きさの基準は,他に比べて高めですが,それは独立変数の数が多いことを考慮したからだそうです(p. 413,慣習的な基準なので根拠は薄い)。”小”,”中”,”大”という基準を直観的に理解するには,2変量の積率相関(ふつうに求めたピアソンの積率相関係数 r と同じもの)と比較すればよいでしょう。この目安に従うと,先ほどの例で出てきたr = 0.2は,“小”から”中”の効果量だといえます。他の検定における効果量は,対応する相関係数と主観的に同じくらいの大きさと考えればよさそうです。
分散分析での効果量の表し方にはいくつもあるようです。まず,関連度(strength of association)の指標をいくつか紹介します。
効果量について,関西大学水本篤先生・竹内理先生の解説記事があります。とても分かりやすいです。(2018.8.6追加) 。
例として,16名の被験者が参加した繰り返し測度(3水準)1要因のANOVAで F(2, 30) = 3.75, p = 0.04 が得られた場合を考えます。
η2(eta squared: イータ二乗) 記述統計量
これは,あるサンプルにおいて,従属変数の全変動の中で,特定の独立変数(ここではAとする)によって説明できる割合をさします。つまり,[要因Aによる変動]/[全体の変動]です。
partial η2,ηp2(partial eta squared: 偏イータ二乗) 記述統計量
これは,あるサンプルにおいて,従属変数の全変動から,特定できる他の要因(主効果や交互作用)による変動を除いた後での,独立変数Aによって説明できる割合をさします。つまり,[要因Aによる変動]/[要因Aによる変動+誤差による変動]です。要因Aの効果を検定するときのF値と自由度から算出できます。
[効果Aの自由度(df1)×効果AのF値]/[効果Aの自由度(df1)×効果AのF値+効果Aの検定に用いる誤差の自由度(df2)]
計算例: (2×3.75)/[(2×3.75)+30] = 0.200
別の計算手続きとしては,F値にdf1をかけてdf2で割り,その値を「その値に1を足した値」で割る。
計算例: 3.75×2/30 = 0.25 と計算し,0.25/(0.25+1) = 0.200
参考文献: Maxwell, S. E., Cameron, J. C., & Arvey, R. D. (1981). Measures of strength of association: A comparative examination. Journal of Applied Psychology, 66, 525-534.
ERP研究でよくある複雑な要因計画のANOVAについては,偏η2がもっとも計算しやすく理解しやすいでしょう(SPSSで分散分析をすると自動的に算出されます)。ERP研究では偏η2を記載した論文の方が多いという印象です。ただし,偏η2を計算しているのに,特に断りなく,η2という記号を使っている場合がよくあります。どちらであるかは,F値と自由度から計算してみれば分かります。また,偏η2には効果量の目安というのはないようです。) (2024.11.3追加,これは間違いでした。Richardson (2011) によれば,偏η2 の目安は,上述の f の目安から算出できます。f は [各条件・群で得られた平均値間の標準偏差]/[母集団の標準偏差] です。偏η2の 小・中・大の効果量の目安は,上述の f の値(0.10, 0.25, 0.40)から,.0099, .0588, .1379に相当すると書かれています。この値は上の表で説明できる変動の割合と一致しています。)Richardson, J. T. E. (2011). Eta squared and partial eta squared as measures of effect size in educational research. Educational Research Review, 6, 135-147. https://doi.org/10.1016/j.edurev.2010.12.001
なお,偏η2の表記ですが,原稿上では p が先になって,「ηp2」と書くようです(たとえば,APAマニュアル第6版,p. 46, Figure 2.1.など)。実際に印刷されるときは,上ツキの2と下ツキのpがほとんど縦一列に並びます。イータ(η)はギリシャ文字なのでイタリックにしません。 (2012.2.13追加)
f2 と偏ω2についての記述は自信がないので削除しました(2010.4.1)。関西大学水本篤先生の解説記事や以下の文献をご覧ください。
参考文献: Kirk, R. E. (1995). Experimental design: procedures for the behavioral sciences (3rd ed.). Brooks/Cole.
効果量は,p値とともに結果に示す以外に,2つの目的に使われます。一つは,メタ分析です。これは,類似した複数の実験結果から,それぞれ効果量を算出したものを総合し,全体としてどのくらいの効果があるかを評価するものです。効果量の信頼区間を推定することもできるようですが,その手順は私には説明できません。もう一つは,パワー分析です。これには,被験者の人数を決めるために事前に行うものと,実験して有意差が得られなかった場合に「本当は差があるのに有意差が得られない確率(タイプⅡエラー)」を事後的に計算するものがあります。パワー(検出力)とは,「差があるものを差があると検出できる確率(1-タイプⅡエラー)」のことです。具体的なパワーの算出方法は複雑で,私には説明できません。G*Power3というフリーソフト(英語版)が利用できるようです。
私は統計学の専門家ではないので,以上の説明には間違いがあるかもしれません。ご指摘いただければ幸いです。
Q4. 統計検定で得られたp値はどのように何桁まで書いたらいいですか?
小数点以下2桁か3桁までを正確に等号を使って書きます(例えば,p = .031)。.001未満のときだけ,p < .001と書きます。このルールは,APAマニュアル第6版(2009; APAによる紹介)で新しく規定されました(p. 114)。”p < .01″といった不等号による記述は,表に限って使われることになりました。なお,p などの統計記号(ギリシャ文字を除く)はイタリックにします。それ以外の数値(t, F, ε, η2など)は2桁まで書きます。APAマニュアル第7版での記載(2023.10.7追加)
論文投稿編
Q1. ERPの論文を書くときに気をつけることはありますか?
基礎編Q6で述べたように,ERPデータを発表するときの注意点をまとめたガイドラインが,心理生理学会(Society for Psychophysiological Research: SPR) から出ています。どの分野でもそうですが,よい論文を書くためには,ベテラン研究者が書いた最近の論文をよく読んで,真似するのが近道です。特に,方法と結果の書き方については決まりごとが多いので,似たような研究テーマの論文をいくつか手元において参照すれば,それほど苦労せずに書けるでしょう。
Q2. 日本語と英語のどちらで発表したらいいでしょうか?
目的にもよりますが,やはり英語で書いた方が利点が多いです。英語で書く利点としては,(1)潜在的な読者が多い(英語を読める人が多いというだけでなく,英語雑誌の方が多くのデータベースに収録されるので他分野の研究者の目にも触れやすい),(2)勉強になる(たとえリジェクトされたとしても,第一線で活躍している専門家から有益なコメントがもらえる),(3)引用論文調査などのサービスが無料で受けられる(Web of Science や Scopus などで,自分の論文を誰が引用したかをチェックできる),(4)英語で論文を書くときに自分の論文を引用できる(日本語の論文を引用するのを嫌がる雑誌もある[内容がチェックできないため]),ということが挙げられます。反対に,英語で書く短所としては,(1)日本人が読んでくれない(英語論文を書くと称賛されるが,中身は面倒なので読まれないことが多い),(2)日本語ほど自由に操れない英語では微妙なニュアンスを表現したり深く掘り下げた考察を行うことが難しい(自分のアイデアを100%は表現しにくい),ということがあります。
また,英語論文は,日本の英文誌よりも,国際誌に投稿した方が,研究面ではプラスだと思います。ある雑誌がどれだけ影響力を持っているかを示す指標にインパクトファクタがあります。これは,Journal Citation Reports(有料)などで検索できますが,たいていは雑誌のページに雑誌自体の宣伝のために書いてあります。ある雑誌に過去2年間に掲載された論文が,その次の1年間に平均何回引用されたかを示す値です。たとえば,ある雑誌に2000年と2001年に掲載された論文が計50本あったとします。そして,それらの論文が2002年にいろいろな雑誌に引用された回数が100回だったとします。そうすると,2002年版のこの雑誌のインパクトファクタは,2.0(100を50で割る) になるわけです。同じ分野の雑誌の影響力を比べるのに使いますが,日本の心理学系の雑誌は,たとえ英文誌でも,きわめてインパクトファクタが低いです(0.1以下)。ERPの論文がよく掲載される国際誌のインパクトファクタは,2-3くらいです(1-2年後に平均2-3回/年は引用される)。どうせ書くのであれば誰かの参考になってほしいですから,その意味でも,国際誌に投稿した方がいいでしょう。
ERPの論文は,心理学の中では比較的構成が単純なので,社会心理学の論文などに比べて,英語でも書きやすいです。最初は,論文を書くスキル(論理の組み立て,段落の構成など)と英文を書くスキルの両方を学ばなければならないので時間がかかりますが,慣れればだんだん早く書けるようになります。将来,英語で論文を書きたいと思っている人は,できるだけ早いうちから英語論文にチャレンジするといいでしょう。いざ英語論文を書こうとすると,ふだん何気なく理解しているはずの英語表現が思い浮かばずにつまずくことが多いものです。そうすると,次回,英語文献を読むときには,研究の内容だけでなく,英語表現も覚えようという目で読むようになります。このような姿勢は,自分で書こうと思って苦労した経験がないかぎり身につきませんから,その意味でも早くから英語で書く訓練をした方がいいでしょう。
英語論文は投稿前に英文校閲に出しましょう。英文校閲をしてくれる業者はいくつかありますが,個人的な印象としては,医学よりも心理学に強い業者に頼んだ方が安心です。ネイティブとはいえ,他の分野(たとえば医学や薬学)の人が,心理学の専門論文を正しく校閲するのが難しいことは,日本語の場合と同じです。ひどい勘違いをされて,校閲されたものをまた手直しなければならない場合も,実はよくあります。私も数社試しましたが,TEXTエディティングサービスがもっとも適切な校閲をしてくれました。一方的な校閲ではなく,疑問があればそれに答えてくれることも魅力です。料金はやや高めですが(3-5万円/本),安心料・サービス料と考えれば納得できます。
英文校閲サービスの値段のランクは,およそ3つに分かれるようです。最も高価なのは,その分野の専門家が校閲するサービスです(200語あたり2000円前後)。中程度は,やや近い分野の専門家が2人で校閲するサービスです(200語あたり1200-1600円)。もっとも安いのは,留学生が大学に提出するレポートの添削に使われるようなサービスです(200語あたり400-600円)。5000語のフルペーパーとすると,それぞれ50,000円,35,000円,13,000円といったところです。私はこれまでに約8社に依頼した経験がありますが,高ければ質のよい校閲が行われるというわけでもないようです(専門的な内容を含むため)。また,校閲結果は100%正解ではなく,専門的な用語・表現については自分で再修正するのがふつうです。自分の英語にある程度自信があれば,リーズナブルな価格のサービスでよいように思います。いくつかの会社へのリンクを掲載しました。(2008.2.18 追記)
Q3. 英語論文を書くときに役立つ文献はありますか?
私が実際に使っている辞書,文法書,心理学関係の書籍を紹介します。
[辞書]コンピュータ上で動く電子辞書を活用しましょう。個人的には,EPWING(電子出版の共通フォーマットJIS-X4081)対応の電子辞書を薦めます。英和辞典・和英辞典だけでなく,文例辞典があると便利です。私が使っているものは,英和辞典として,小学館ランダムハウス英語辞典(これは単体ソフト)と研究社リーダーズ+V2(EPWING版)を,和英辞典として,研究社新和英辞典第4版(EPWING版)を,文例辞典として,研究社新編英和活用大辞典(EPWING版)とビジネス技術実用英語大辞典第4版(EPWING版)を使っています。ランダムハウス英語辞典以外は,ひとつの検索ソフトを切り換えて使えます。これらの電子辞書についての詳細は,日外アソシエーツのホームページを参照してください。また,英英辞典としては,Merriam-Webster’s Collegiate Dictionary (11th ed.) があると便利です。アメリカ心理学会の投稿の手引き (下記[心理学関係の書籍] 参照)では,略語は初出時に省略せずに書くことになっていますが,この辞書にnounとして載っている語(abbreviationと書いていないもの)は単語として説明なしに使ってよいとされています(p. 105)。たとえば,IQ,REM,ESP,AIDS,HIVなどがあります。EEGは載っていますが,abbreviationと書いてあるので,初出時には省略せずに書きます。event-related potential (ERP),reaction time (RT),short-term memory (STM)などは省略形としても載っていないので,初出時に省略せずに書きます。
[文法書]どれも似たり寄ったりで,かゆいところに手が届く解説がある本は少ないです。私が使っているのは,杉山忠一(1998)「英文法詳解」学習研究社です。冠詞の反復と名詞の単数・複数形について,私が調べた本のなかで唯一説明されていました。例えば,the first and the secondに続く単語は複数か単数かといった問題です。2つあるから複数がよいように思えますが,正解は単数ということです(the first and the second chapter)。理屈としては,the first chapter and the second chapterの最初のchapterが省略されたと考えるのだそうです(p. 63)。大学受験向けの本ですが,十分役に立ちます。
[心理学関係の書籍]英語では,アメリカ心理学会の投稿の手引き(Publication manual of the American Psychological Association (6th ed.) (2009), APAによる紹介)が欠かせません。2009年に第6版が出版され,本の厚さが3分の2位になりました。その他に参考になるのが,イエール大教授のRobert J. SternbergのThe psychologist’s companion: A guide to scientific writing for students and researchers と Guide to publishing in psychology journals でしょう。文法に関しては,Bellquist, J E. (1993). A guide to grammar and usage for psychology and related field. が参考になります。日本語では,シュワーブ他 (1998). 初めての心理学英語論文 北大路書房を読んでもいいかもしれません。最近では,ラッカム・原 (2004). 心理学のための英語案内 サイエンス社が出版されましたが,著者のあとがきにもあるように,あまり実用的ではありません。
論文を書くための本ばかり読んでいても,論文は書けません。手元にデータがあるならば,まずは書き始めることをお薦めします。
Q4. 英語の句読点の後にスペースはいくつ必要ですか?
英文タイプでは,カンマ(,)の後は1スペース,ピリオド(.)の後は2スペース空けるのが慣例です。英文校閲に出すと,この点を直されることがあります。しかし,アメリカ心理学会の手引き(第5版, 2001)では,「どの句読点の後も1スペース」と規定しています(p. 290)。印刷原稿を作るときに1スペースの方が処理しやすいからではないかと想像します。日本心理学会の執筆・投稿の手引き(1991年改訂版)では,この点について明記していませんが,参考資料の見本原稿をみると,ピリオドの後は2スペースになっています。論文の投稿規程に従うのがよいでしょう。
アメリカ心理学会の投稿の手引き(第6版, 2009, 日本語版)では方針が変わり,「原稿では,文末のピリオド後に2スペースいれると読みやすくなる」と書いています(4.01, p. 88)。この箇所は,第1刷(first printing)では「2スペースいれる」となっていたのですが,出版後にルールから推奨(recommndation)に変更されました。第1刷には数十ヶ所の間違いがあるので,注意が必要です (訂正箇所一覧PDF)。私も購入しなおしました(2012年7月時点で第6刷)。日本語版ではしっかり訂正されていました。
細かいことですが,APAスタイルでは,雑誌と巻をイタリック(斜体)にします。その前後ではカンマもイタリックにするのが正しいようです。
正: … Psychophysiology, XX, YY-ZZ.
誤: … Psychophysiology, XX, YY-ZZ.
ただし,号が入るときは,後のカンマはイタリックにはなりません(例: …, XX(Y), Z)。
(巻と号の間にスペースはいらない)。
目をこらさないと分からないくらい,細かいルールです。
Q5. 図を作るのに適したソフトウェアは何ですか?
図を作成するソフトウェアはいろいろありますが,私はKyPlot(カイエンス)を薦めます。数年前までベータ版として無償公開されていましたが,現在は有償です。かなり高いですが(たとえば1ライセンスで通常版8万円,学生版2万円ほど),その値打ちはあります。私がこれまで試したグラフ・画像作成ソフトは,Excel(Microsoft), DeltaGraph(日本ポラデジタル株式会社), CorelDraw(メディアヴィジョン),The Graph(アイフォー), Origin(OriginLab)などですが,これらの中で一番融通が効き,妥協なしにイメージどおりの図が描けます。グラフだけでなく,線画もきれいに作れます。またメールによるサポートも迅速にしてくれます。(残念ながら2011年末に販売終了しました。現在はありがたいことに無償で Kyplot 6.0が提供されています![こちら])
Q6. 図を画像ファイルにするよい方法はありませんか?
最近は,図を画像ファイルで送るように求められることが多いです。以前は,印刷した図を送れば,出版社がスキャナーで取り込んでくれましたが,現在は画像ファイルでの提出が推奨されています。また,オンラインで投稿する雑誌では,図を画像ファイルにできなければ投稿さえできません。紙に印刷した図をスキャナで取り込む方法もありますが,傷やゴミが入ってなかなかきれいにできませんし,元々デジタルデータなのに一度アナログ(紙)に変換して再びデジタル(画像ファイル)にするのはスマートではありません。
KyPlotでは,エクスポート機能により,画像ファイルを作成できます。しかし,大きなファイルになると,高解像度ではエクスポートできません(本体のメモリに依存する)。
Powerpointの設定を変えることで,高解像度の画像ファイルとして保存することもできます。こちらのサイトなどが参考になります。
作成した画像ファイルを開いて,不要な余白を削ったり回転させたりするには,フリーウェアのIrfanView(著作権 Irfan Skiljan氏)がお薦めです。メニューを日本語に変更するための追加ファイルもあり,簡単な加工作業をするには十分です。

